Blobcodes, or how I discovered a way to code information in a topological invariant of binary images and obtain arbitrarily deformable, easily computer-recognizable barcodes. A patent was filed by my university, a prototype made and presentations given, but later abandoned due to prior art in some obscure conference, together with hopes of a start-up.
The story
In 2004, while I was doing my Ph.D. at LIAFA (Université Paris VII), I invented a class of easily computer-recognizable codes capable of holding amounts of data similar to barcodes, but that can withstand deformation.
Hopes of industrialization
I did research in the library and on the net to see if this had been discovered before. I didn't find anything, and the head of my lab suggested that I get in touch with the university's valorisation bureau (BVRI). I then proceeded to develop the invention, and thanks to a Firewire camera lent by the BVRI, I built a real-time demonstration prototype. I wrote the draft of the patent application. It took ages for the law firm to write it, and the university applied for a patent in 2005.
The patent application
Method of coding in graphic form is the patent application that was filed by Université Paris 7 for my "blobcode" invention which I had while doing my thesis at LIAFA .
Blobcodes (at the time we dubbed them "T-codes", T for topological) being recognized in real-time. Note how the lens distortion does not affect recognition. Of course clipping a half or a third of the code renders it unreadable.
With my friend Ferda Tartanoğlu we decided that this could lead to a start-up, so we searched industrial partners with the BVRI. There was some interest. Meanwhile, the Patent Commission gave its report, which was generally positive. (Like most patent applications, there were some unrelated papers that the reviewers thought might constitute prior art. They didn't find the conference paper.)
Prior art
Unfortunately, Ferda discovered that there was prior art in a small 2004 conference. Because of this and due to lack of sufficient industrial interest, and given the costs involved, the patent application was left at the PCT phase.
What are Blobcodes?
In 1999, I was studying in the mathematics department of Université Montpellier II. My flatmate, Benjamin Rey, was studying biology, and he brought home some large cockroaches in a box. As I was playing with machine vision using a black and white surveillance camera at the time, I thought that having my computer automatically track those cockroaches and recognize them individually could be interesting. Since the insects were visually indistinguishable, this meant marking them somehow. Bar codes came to mind, but how would I attach them to the back of the insects? Also, given my camera's resolution, it would not be possible to read the codes. Bar codes are also difficult to read. I knew of matrix 2D codes but if I put a sticker with a matrix code on the back of one insect, the code would be distorted and probably unreadable.
Therefore I needed codes with the following properties: Net information capacity of at least a few bits, to distinguish a few insects, Readable in very low resolution, Can withstand non-linear distortion, Easy to decode in real time on a low-power computer.
I found the solution five years later.
Problems in pattern recognition
Pattern recognition in images is a difficult problem. The principal difficulty is that your patterns can be subject to a great number of transformations:
-
Color and luminosity transformations. The registered brightness levels of an object are generally unpredictable, save in completely controlled settings. Shadows and illumination can make the levels non-uniform.
-
Noise and dirt means that even with perfect registration, having an exact match is hopeless, and you cannot rely on small features.
-
Translation is the simplest of transformations. If we had only translations, machine vision would be as simple as string matching or basic 1D signal processing.
-
Embedding. By this, I mean that your pattern is surrounded by non-patterns. This might not sound like a transformation, but unless you are in a very controlled setting, your pattern will be lost within a sea of unrealted things.
-
Rotation can be easily solved if your center of rotation is known. But it is not, since usually you also have translation.
-
Scaling is more complicated. Multi-resolution tricks help, but generally you must rely, at some point, on something that is scale-dependent: atomic features.
-
Perspective, which generalizes scaling, rotation and translation, makes the recognition of perspective-invariant features (such as lines or special points or patterns) almost mandatory.
-
Distortion (lens and physical).
-
Occlusion is the dreaded beast of machine vision. It is extremely difficult to have patterns that can be machine-recognizable while partially are obscured.
The problem is that you cannot combine solutions to each individual transformation to get a solution for the combination of transformations. In other words, it is easy to solve for translation alone, or rotation alone, but if you combine both and add embedding it gets much more difficult.
Blobcodes can be subject to arbitrary topological distortions and still retain their information. All these codes are still perfectly readable. The algorithm doesn't even know that they are "distorted".
A topological invariant for images
While abstract toplogies can be defined for anything from programs to functional spaces, toplogy started in ordinary geometry as the study of characteristics that are invariant under continuous deformations. Intuitively, two objects can be considered topologically equivalent if you can transform a putty replica of one into a putty replica of the other by remolding, subjected to the constraint that:
-
You do not create new holes, for instance by neither tearing nor by connecting the ends of a tube,
-
You do not destroy existing holes.
Thus, a non-trivial geometrical topology would be resistant to most of the transformations (scaling, rotation and perspective). A digital image is a basically matrix of real values, with no intrinsic topology save for the usually 4-connected pixel grid. However, if we binarize the image, our pixels are partitioned into two sets : the black pixels, and the white pixels. Now remove edges that connect pixels of different colors. You now get an unconnected graph, with black connected components and white connected components. However, the black and white components have a strictly hierarchical containment relationship. (That wouldn't be the case with 3 or more colors.) Therefore, from our binary image, we have extract a connected component tree .
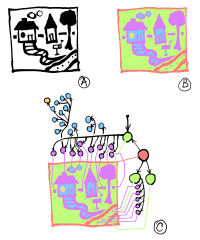
Consider the following picture.
Assuming the picture is initially white, our tree is made of a white node corresponding to the whole picture, then we have a set of black components (the tree, the houses, the road, etc.) which in turn contain white components (the houses contain their door), and so on down to the atomic components.
In (a) we have our initial black-and-white picture. In (b) we color the connected components of the pictures according to their depth in the component tree. The white border of the picture is not taken into account. Our tree starts at the border, colored in red. The immediate children of the border are in green (three of them.) Each green children has zero or more mauve children. The houses and the two puffs of smoke contain blue components. The blue component of the left house has even a yellow component in it: this is the deepest node in our tree. The resulting tree is shown in (c).
Finding subtrees
The subtree corresponding to our codes will be contained in the unspecified, large tree of the whole picture. Therefore the subtree must be dissimilar from the subtrees of its surroundings. In other words, we need to use codes whose subtrees are statistically unlikely in random pictures. Fortunately, it turns out that ordinary pictures either do not contain deep trees, or contain deep trees whose number of nodes grows slowly with depth. Thus codes whose number of children grows "exponentially" with depth are easily recognizable. (I put "exponentially" in quotes because you cannot make a conclusion on the asymptotic behaviour of a function from a finite observation.)
Of course, selecting a sparse subset of the possible large trees, for instance by adding some kind of checksum, will help cut down the false positives. But unless we want to search for a small number of specific trees, we need a way to convert an arbitrary bitstring into a tree.
It is possible to take an existing design and, by slight modifications, turn it into a valid blobcode. Here, an amblem inspired from the arms of Calgary University has been manually transformed into a blobcode.
Encoding information in the tree
The trees being unordered, efficiently encoding information in them is an interesting combinatorial and algorithmic problem. The first trick is to "uncommutatize" a tree by adding special subtrees to help distinguish left and right nodes. This is the solution described in my patent application. It is not very efficient. A more space-efficient solution is to use some kind of combinatorial encoding. The Matula encoding is a bijection between integers and unordered trees, based on prime number decomposition. It is quite expensive to compute (since basically you are factoring over and over... and no, better factoring algorithms don't help much since we are factoring very small integers), but it works. So that's what I implemented.
- Berke Durak